myspace viral growth numbers
viral growth is often referred to the tipping point popularised and applied to daily life by malcolm gladwell
“as everyone from academics to engineers to tech reporters to web 2.0 bloggers try to apply formulas like metcalfe’s law and reed’s Law to social networking, i could not find a good timeline of actual myspace growth statistics.”
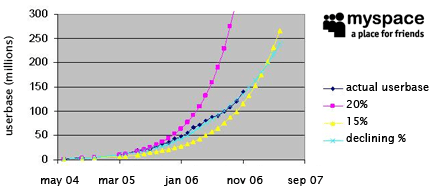
joe was taking data from various sources like press releases, news articles, and blog entries to plot this graph.
“the curve-fit in light blue is what i’m calling the declining percentage model. if you take the top chart and calculate monthly percentage growth, you’ll see that average growth was roughly 20% in the first 12-month period, 15% the next year, and 10% in the following year.
the declining % represents “true” viral growth – the kind of organic growth that happens after a marketing campaign where planned (and unplanned) distribution channels were already exhausted. i base this claim on 3 reports that documented myspace’s initial launch campaign. all reports agree that myspace ended its aggressive marketing campaign to seed the network with its first couple million users in ~q2 of 2004.
these numbers don’t disprove or prove metcalfe’s law. metcalfe’s law is conceptual in nature and is expressed in the value domain as opposed to the time domain.”
the bottom line is that even the most succesful network can not grow exponentially over a long period of time even after hitting the tipping point, the declining percentage represents the more realistic “true” viral growth.
(via joe suh at mychurch.org)
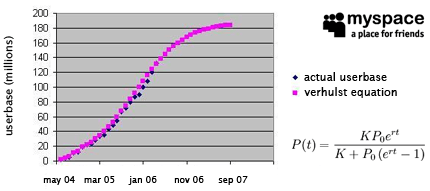
update – november 21. 2006 at 11:03: as joe’s post was on the front page of digg.com for some time other users indicated that a logistic function like the verhulst equation should be used to model the growth.
“we now get a slightly more conservative projection and curve-fit. qualitatively, a logistic function reflects how the initial stage of growth is approximately exponential, then slows down asymptotically as competition arises or the product matures. the verhulst formula, in particular, is often used to model population growth that takes into account the size of the population and the amount of available resources.”
[tags: myspace, myspace.com, viral, growth, viral growth, gladwell, metcalfe]